Komplexní čísla - úvod
Autor: Kub@z | 16.1.2005 |
Tento článek popisuje co jsou to komplexní čísla (pro ty co neví, o co jde - počítá se s odmocninou z -1) a základní operace s nimi
Na začátek chci říci, že tento článek je určen pro žáky základní školy nebo pro studenty prvního a druhého ročníku střední školy. Pro ostatní zjevně nemá smysl, protože ti už to na střední škole probrali a já zde budu popisovat opravdu pouze naprostý základ.
Takže nejdříve by to asi chtělo popsat, co to komplexní čísla jsou. Komplexní čísla jsou rozšíření reálných čísel. Množina komplexních čísel se značí C a reálná čísla (R) jsou její podmnožinou. Co je tedy ono rozšíření? Co je v C navíc? Ukážu to na malé rovnici:
x2 + 1 = 0
I žák páté třídy dokáže upravit na:x2 = -1
Takže logicky dojdeme k závěru, že zadaný příklad nemá v R řešení, protože neexistuje žádné reálné číslo, které by na druhou mělo kladnou hodnotu. V komplexních číslech ovšem řešení má. Označme si jako "i" prvek, jehož druhá mocnina je -1. Pak platí:i2 = -1
"i" je tzv. imaginární jednotka. Dá se zapsat jako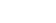
i2 = -1
i3 = i * i2 = -i
i4 = i2 * i2 = -1 * -1 = 1
i5 = i4 * i = 1 * i = i
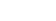 pro všechna přirozená "n"
pro všechna přirozená "n"
a + bi
kde "a" a "b" jsou reálné konstanty. Zkusme spočítat třeba tento příklad: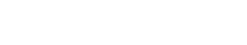
x + y = (a + bi) + (c + di) = (a + c) + (b + d)i
x - y = (a + bi) - (c + di) = (a - c) + (b - d)i
x * y = (a + bi)*(c + di) = ac + cbi + adi + bdi2 = (ac - bd) + (ad + cb)i
Budeme potěšeni, pokud vás zaujme také reklamní nabídka


