Rainbow tables tajemství zbavené
Autor: .cCuMiNn. | 1.2.2015 |
S duhovými tabulkami nebo-li Rainbow tables se dnes již střetáváme naprosto běžně. Každý tak dokáže říci, k čemu tyto tabulky slouží a jak je lze použít. Málokdo už ovšem ví, jak jsou tyto tabulky ve skutečnosti generovány, jak jsou uloženy, a jak jsou nakonec aplikovány při louskání hashů. Nebude jistě od věci si tuto teorii blíže představit.
Zažité vnímání Rainbow tables je takové, že jde o tabulku s vygenerovanými páry heslo / hash pro všechny možné kombinace z požadované množiny znaků se zadanou délkou hesel. Kolik by v takové tabulce muselo být řádků, zjistíme snadno ze vzorce množina^délka_hesla. Pro čtyřznaková hesla tvořená pouze znaky malé abecedy a..z by řádků bylo 26^3 = 17.576. Počet kombinací označujeme výrazem keyspace.
Malý úryvek z takové tabulky by mohl vypadat například takto:
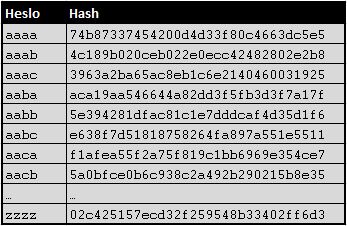
V případě požadavku na prolomení hashe aca19aa546644a82dd3f5fb3d3f7a17f bychom se jednoduše zeptali této tabulky a téměř okamžitě bychom dostali odpovídající heslo aaba. Zní to logicky, ale pojďme si nyní vzít příklad devítimístných hesel tvořených z písmen malé i velké abecedy a čísel. Jak velký by byl její keyspace, a kolik řádků by tedy měla výsledná tabulka? Přichází čas na trochu počítání. Možných variací máme 62^9 = 13.537.086.546.263.552, což je i odpovídající počet řádků výsledné tabulky. Pokud bychom takovou tabulku chtěli uložit do textového souboru, potřebovali bychom pro každý řádek 7 bytů na uložení hesla a budeme-li se bavit o hashovací funkci MD5 pak i dalších 32 bytů pro uložení hashe (ve skutečnosti je MD5 tvořena pouze 16ti byty, ale pro zjednodušení, zůstaneme u ukládání v txt podobě). Po aplikování jednoduché matematiky nám vychází velikost výsledné tabulky 13.537.086.546.263.552 * (7+32) = 527.946.375.304.278.528 bytů, tedy 480.164 TB. Rainbow tabulku, která obsahuje všechna mixalpha-numeric hesla do délky 9ti znaků si ale můžeme stáhnout ze stránek https://www.freerainbowtables.com/tables2/ o velikosti pouhého jednoho terabytu. Námi vypočtené hodnoty tedy vychází cca 500.000x větší, než jaká je velikost tabulky, kterou si můžeme stáhnout. Jak je to možné, a jak to s těmi Rainbow tables tedy ve skutečnosti je?
Rainbow tabulky nemají a přesto mají pouze dva sloupce
Příklad tabulky, který jsme si uvedli výše, obsahoval pouze dva sloupce obsahující kombinaci hesel a odpovídajících hashů. Toto by sice mohla být také Rainbow tabulka, ale dala by se použít pouze na velice krátká hesla. Tabulku o dvou sloupcích pro devítimístná hesla bychom totiž asi těžko někam uložili, viz. náš předchozí výpočet. Pro lepší pochopení následujícího textu budeme pro začátek vše hodně zjednodušovat. Začneme například tím, že budeme předpokládat Rainbow table čtyřznakových hesel tvořených pouze z písmen velké abecedy, kde i hashe budou pouze čtyřznakové ze stejné množiny znaků. Taková tabulka by vypadala takto:
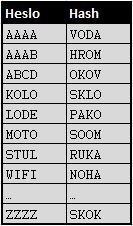
Z této tabulky vyplývá, že hashe se musí dříve nebo později objevit nejen v pravém sloupci, ale i ve sloupci levém, který obsahuje všechny variace čtyřznakových řetězců. Proto se dá říci, že takto vypadající hash může být nejenom hashem, ale může být současně i heslem.
Pojďme si tedy vytvořit tabulku o více sloupcích, kde každý další sloupec je vytvořen zahashováním hesla z předchozího sloupce:
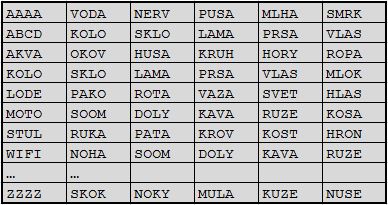
Vysvětlení: Zahashováním hesla AAAA nám vznikne hash VODA, který použijeme jako heslo a znovu jej zahashujeme. Zahashováním hesla VODA nám vznikne hash NERV, který opět použijeme jako heslo a po zahashování dostáváme hash PUSA. Stejně budeme pokračovat až na konec řádku, a celý postup budeme opakovat i pro všechny řádky tabulky.
Co jsme tím získali? Zatím to vypadá, že nic, ale ve skutečnosti nám bude stačit, když si ponecháme pouze první a poslední sloupec a všechny vnitřní sloupce (kterých může být i desetitisíce) vyhodíme. Dovůdem, proč můžeme vnitřní sloupce vyhodit, je skutečnost, že jsme schopni si tyto sloupce kdykoliv dopočítat. Po tomto vypuštění získáme tabulku, která bude vypadat takto:
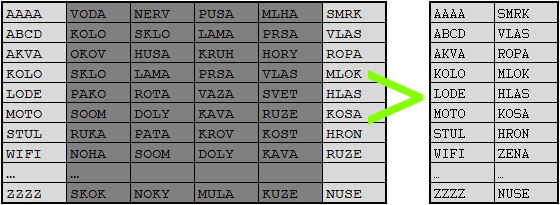
Vyhledáváme v rainbow tables
Nyní si představte, že se vám do ruky dostal hash KROV a vy se budete snažit najít v tabulce odpovídající heslo. K dispozici máme následující Rainbow tabulku, o které víme, že z ní byly vypuštěny 4 sloupce.
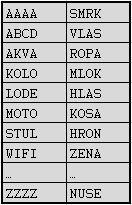
Postup při vyhledávání bude následující:
- 1) Vyhledáne, zda se ve druhém (posledním) sloupci tabulky nachází náš hash KROV.
- 2) Pokud v něm hash nenajdeme, pak náš hash KROV zahashujeme, čímž získáme hash KOST.
- 3) Vyhledáme, zda se ve druhém (posledním) sloupci tabulky nachází náš hash KOST.
- 4) Pokud v něm hash nenajdeme, pak náš hash KOST opět zahashujeme, čímž získáme HRON.
- 5) Vyhledáme, zda se ve druhém (posledním) sloupci tabulky nachází náš hash HRON.
- 6) Tentokrát již budeme úspěšní a hash HRON v posledním sloupci najdeme, čímž získáme řádek, na kterém se bude nacházet i naše heslo.
- 7) Víme, že z Rainbow tabulky byly vypuštěny čtyři vnitřní sloupce, a že pro získání hashe HRON v posledním sloupci, jsme museli původní hash KROV dvakrát zahashovat.
- 8) Odtud 4 - 2 = 2, tedy 2x budeme muset zahashovat heslo z prvního sloupce, abychom získali heslo odpovídající hashi KROV.
- 9) Vezmeme tedy heslo STUL a dvakrát jej zahashujeme STUL -> RUKA -> PATA.
- 10) PATA je heslo, které jsme se na začátku pokoušeli získat. Jde totiž o heslo odpovídající hashi KROV.
Redukční funkce
Nyní si patrně říkáte, co to tu plácám za nesmysly. Vždyť je každému jasné, že hashe nejsou čtyřznakové, a že jsou tvořeny z úplně jiných znaků, než které jsme v naší tabulce používali. Máte samozřejmě pravdu, a abychom vše uvedli na pravou míru, budeme si muset říci něco o redukčních funkcích. Ty slouží právě k tomu, aby převedly skutečný hash na hash, který svou délkou a množinou použitých znaků odpovídá požadovanému tvaru hesel.
Při generování tabulky tedy ve skutečnosti budeme postupovat takto (stále zjednodušeno):
- 1) Před samotným generováním tabulky musíme znát:
- a. Hashovací algoritmus, pro který tabulku vygenerujeme. V našem případě MD5.
- b. Délku hesel, pro které má být tabulka vygenerována. V našem případě 4 znaky.
- c. Množinu znaků, z nichž se mají jednotlivá hesla skládat. V našem případě písmena velké abecedy.
- 2) Množinu znaků, ze kterých mají být hesla tvořena si vypíšeme a očíslujeme

- 3) Nejprve pomocí generátoru vygenerujeme hesla do prvního sloupce naší budoucí Rainbow tabulky.
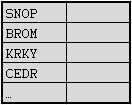
- 4) Následně vezmeme heslo z prvního sloupce SNOP a zahashujeme jej hashovacím algoritmem, pro který je tabulka generována. V našem případě MD5.
- 5) Získáme tak hash 2b6c79342c50ac0fc44911ae2f701909.
- 6) Hash rozdělíme na jednotlivé byty a odřízneme si pouze tykový počet bytů, jak dlouhé má být naše heslo. V našem případě požadujeme 4 znaky, takže si z MD5 hashe vezmeme pouze první 4 byty.
| 2b | 6c | 79| 34 |2c | 50 | ac | 0f | c4 | 49 | 11 | ae | 2f | 70 | 19 | 09 |
| 2b | 6c | 79| 34 |
- 7) Každý byte je vlastně číslo v šestnáctkové soustavě, tak si je pojďme převést na desítková
2b -> 43 6c -> 108 79 -> 121 34 -> 52
- 8) Protože je námi požadovaná abeceda tvořena 26ti znaky, tak si rovnou zjistíme zbytky po dělení jednotlivých bytů dvacetišesti
43 % 26 = 17 108 % 26 = 04 121 % 26 = 17 52 % 26 = 00
- 9) Získané hodnoty nyní převedeme pomocí vypsané abecedy na konkrétní znaky podle pořadí znaků v abecedě
17 = R 04 = E 17 = R 00 = A
- 10) Z hesla SNOP rázem získáváme hash RERA, který je dlouhý požadovaný počet znaků (4) a současně je tvořen pouze z požadované množiny znaků (A..Z).
- 11) Celý postup opakujeme až do konce řádku a teprve hodnotu v posledním sloupci uložíme.
- 12) Celý postup opakujeme pro všechny řádky
Tak už je vám jasné, jak se Rainbow tabulka generuje? Upozorňuji, že jsem pro lepší pochopení problematiky celý postup zjednodušil. Ve skutečnosti jsou redukční funkce mnohem složitější.

RF – redukční funkce
Kde vzaly Rainbow tabulky svůj název
Podíváme-li se nyní znovu na tabulku, kterou jsem již jednou použil dříve, můžete si v ní všimnout kolize u hashů KOLO nebo SOOM.

Například hash SOOM vznikl jednou z hesla MOTO a podruhé z hesla NOHA. Na tom není nic neobvyklého a ve skutečnosti se v Rainbow tabulkách s podobnými kolizemi střetneme hodně často. Je zde ovšem jeden problém, který těmito kolizemi vzniká a to ten, že se po kolizi již opakuje veškerý obsah všech následných sloupců až do konce řádku. V uvedené tabulce tedy najdete 2x nejenom heslo SOOM, ale i DOLY, KAVA a RUZE. Když si uvědomíme, že sloupců může mít Rainbow tabulka i desetitisíce, pak bychom zbytečně prováděli desetitisíce výpočtů opakovaně, a tím bychom zbytečně plýtvali výpočetním výkonem. Ve skutečnosti je tedy v každém sloupci použita jiná redukční funkce, a tím pádem nám jednou z hesla SOOM vznikne DOLY, ale v jiném sloupci nám použití jiné redukční funkce vytvoří ze stejného hesla slovo SLZA.
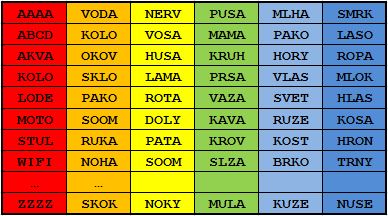
V tabulce jsem se snažil různými barvami naznačit použití odlišných redukčních funkcí v jednotlivých sloupcích. Toto barevné rozlišení nám přitom vytvořilo i pěknou duhu, čímž jsme se dostali i k tomu, kde Rainbow tables získaly svůj název.
Dva extrémy
Pokud jste při čtení textu dávali dobrý pozor, možná vám došlo, že tabulka o pouhých dvou sloupcích ze samého začátku článku, byla extrémem Rainbow tabulky, která byla exterémně dlouhá, ale současně bylo i extrémně rychlé vyhledávání v ní. Během čtení vás ale mohl napadnou i opačný extrém - tedy Rainbow tabulka o miliardách sloupců, která by ve výsledku vypadala takto:

Máme zde tedy dva extrémy:
Který z extrémů zvolit? Odpověď na tuto otázku je jednoduchá: Ani jeden z nich. Při tvorbě Rainbow tabulek budeme sahat ke kompromisu. Budeme se snažit vytvořit tak vysokou tabulku, aby se nám vešla na disk, a současně tak širokou, abychom v ní byli schopni v rozumném čase vyhledávat.
Winrtgen
Snad mě uživatelé systému Linux neukamenují, když v praktické části zmíním windowsovský nástroj Winrtgen, jenž je součástí instalace známého multifunkčního nástroje Cain & Abel. Tento nástroj vám pomůže nejen při vytváření vlastních Rainbow tabulek, ale hlavně si pomocí něj můžete snadno vyzkoušet hledání vhodného kompromisu mezi výškou a šířkou Rainbow tabulky.
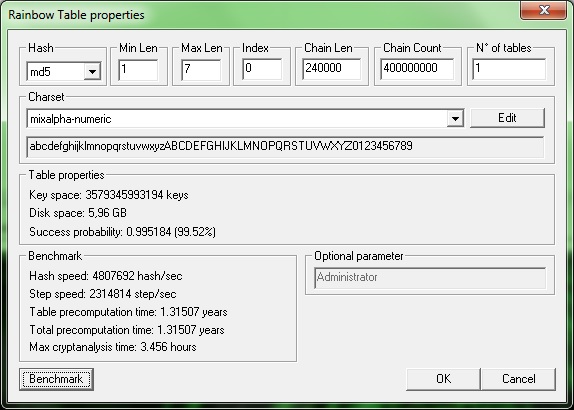
- 1) Po spuštění nástroje Winrtgen klikněte na tlačítko Add Table
- 2) Z rozevíracího seznamu Hash zvolte požadovaný algoritmus
- 3) Z rozevíracího seznamu Charset zvolte množinu znaků, které chcete používat ve svých heslech
- 4) V polích Min Len a Max Len uveďte délku hesel (počet znaků od-do)
- 5) Pole Chain Len udává šířku tabulky (počet slouců)
- 6) Pole Chain Count udává výšku tabulky (počet řádků)
- 7) Velice důležitý je údaj Success probability, který udává pravděpodobnost, že ve výsledné tabulce najdete konkrétní heslo. Při tvorbě tabulek se tedy snažte dosáhnout alespoň 99% úspěšnosti.
- 8) Údaj Disk space zobrazuje velikost, kterou výsledná tabulka zabere na disku. Tato hodnota se bude zvyšovat, pokud budete zvyšovat výšku tabulky. Naopak, jak správně předpokládáte, nebude se zvyšovat se zvyšujícím se počtem sloupců, protože, jak již víte, ukládá se pouze první a poslední sloupec.
- 9) Tlačítkem Benchmark následně otestujete rychlost vašeho počítače a v údaji Max cryptoanalysis time zjistíte čas, který bude potřebný pro nalezení hesla v tabulce. Tento čas není naopak příliš závislý na výšce tabulky, ale razantně se bude prodlužovat při navyšování počtu sloupců.
- 10) Samotnou kapitolou je pak údaj Table precomputation time, který udává, kolik času bude na vašem počítači potřeba pro vygenerování tabulky. Až tuto hodnotu uvidíte, pravděpodobně na generování Rainbow tabulek vlastními silami zanevřete a stáhnete si již vygenerované tabulky z webu.
Pokud si budete s hledáním vhodného kompromisu chvíli hrát, zjistíte, že na vašem hardwaru budou reálně použitelné tabulky do maximální velikosti 9 až 10 znaků. Pro delší hesla nebudete mít s největší pravděpodobností dostatečně velké úložiště, nebo nebudete mít ve vašem životě dostatek času, abyste se hledaného hesla dočkali.
Z uvedeného vyplývá, že Rainbows tables nejsou všemocné, a pokud uživatelé použijí dostatečně dlouhá a silná hesla, tak i takový zázrak, kterým jsou duhové tabulky, bude naprosto bezbranný.
Budeme potěšeni, pokud vás zaujme také reklamní nabídka


